| Меню сайта |
|
 |
| Мини-чат |
|
|
|
| Наш опрос |
|
|
| Статистика |
Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
|
| Форма входа |
|
|
|
 | |  |
| Главная » Архив материалов
На нашем форуме в теме "Девайсы с геометрией ленты Мёбиуса" размещу концепт новой катушки с мудреным названием "Нескомпенсированная бифилярная катушка Мёбиуса". Сразу оговорюсь, что по разным причинам 3-D графики не будет. Будут использованы старые иллюстрации и словесное описание.
Катушка обещает получиться.весьма интересной и заманчивой. Если кого заинтересует, дайте знать. Смогу предложить конкретную технологию её изготовления. Принципиальных трудностей в её сборке нет. Но некоторые нюансы присутствуют.
P.S. Сделано. Читать на форуме:
Просмотров: 465 |
Добавил: aleksandr128 |
Дата: 03 Октябрь 2013
|
|
 А что если взять и изготовить индуктор в виде сферы? Но не просто сферический индуктор, а индуктор в индукторе. Т.е. внутри одного сферического индуктора будет расположен второй индуктор по меньше. Но внутренний индуктор будет иметь направление намотки провода в противоположную сторону внешнего индуктора. Внизу (под спойлерами) показан такой необычный девайс в аксонометрических проекциях, а на цветных изображениях разными цветами, для наглядности, показан внешний (желтым цветом), внутренний (зелёным цветом) и перемычка (красным цветом) соединяющая внешний и внутренний индукторы в одну электрическую цепь.
Такие индуктора можно подключать и без перемычки (выделена красным цветом) по отдельности. Подавая на них разного рода модулирующие сигналы или проводить опыты с подачей как переменного + постоянного токов (на внешний , к примеру переменный, а на внутренний постоянный). Вобщем, при исключении перемычки, вариантов подачи напряжений и сигналов может быть несколько.
|
На этом видео показано, что произойдёт если разрезать кольцо Мёбиуса. А так же продемонстрирована пара фокусов при таких манипуляциях с кольцом Мёбиуса. Автор - aleksandr128
Просмотров: 308 |
Добавил: Tyomich |
Дата: 24 Сентябрь 2013
|
|
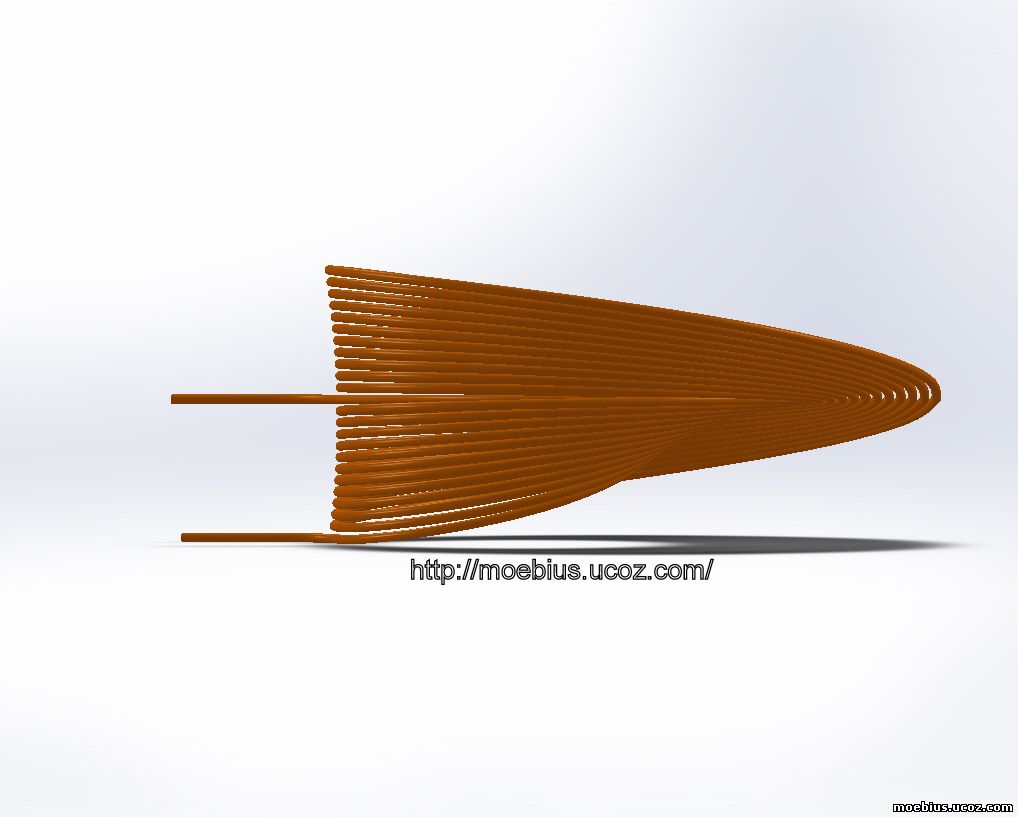 На изображениях показана, в разных ракурсах, катушка (соленоид), наследующая геометрию кольца Мёбиуса. По сути, в плоском (имеется в виду, когда витки уложены в один ряд) исполнении, данный соленоид полностью наследует геометрию ленты Мёбиуса. Следуя принципам топологии, данную катушку Мёбиуса можно отнести к ленте Мёбиуса торового исполнения.
Ниже (под спойлерами) показана данная катушка в аксонометрической проекции и этапы изготовления (намотки) данного девайса. Для упрощения восприятия, каждый цикл намотки выделен отдельным цветом.
Просмотров: 847 |
Добавил: Tyomich |
Дата: 16 Сентябрь 2013
|
|
Построение переплетений из нескольких торовых моделей лент Мёбиуса невозможно, потому как нельзя избежать их взаимных пересечений, не выходя за пределы базового тора. Но эта проблема легко решается "плоскими" (полосковыми) моделями ЛМ. Широко известна модель переплетения двух однонаправленно закрученных "плоских" ЛМ. Изображение такой модели встречается даже среди рисунков на полях. Следуя алгоритму построения таких переплетений, возможно построить модели с переплетением трех и более "плоских" лент Мёбиуса. 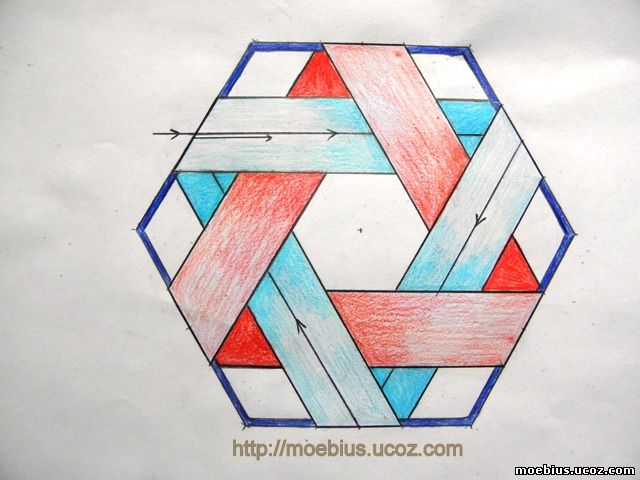  Один маленький нюанс. Когда "гуглил" картинки по ключевым словам "mobius strip", то встречал переплетения только однонаправленно закрученных ЛМ. Решил как-бы восполнить этот пробел и представляю модель переплетения двух противоходно закрученных "плоских" лент Мёбиуса.
Просмотров: 438 |
Добавил: aleksandr128 |
Дата: 15 Сентябрь 2013
|
|
Еще один из возможных девайсов с геометрией ленты Мёбиуса - бифиллярная катушка Мёбиуса. Картинка очень информативна и практически не нуждается в объёмных комментариях. Как и в случае с "обычной"катушкой Мёбиуса, намотка такой бифиллярки сдвоенным проводником начинается от середины (от средней линии).
Особенности намотки: сдвоенный проводник не будет все время укладываться парой, а в конце первого цикла раздвоится и с каждым новым циклом ветки проводника будут удаляться друг от друга. Для того, чтобы этот принцип намотки Мёбиусной бифиллярки стал более понятен, ветки проводника окрасили в разные цвета.
Просмотров: 922 |
Добавил: aleksandr128 |
Дата: 07 Сентябрь 2013
|
|
Уважаемые друзья.
Хочу еще раз обратить Ваше внимание на то, что значительная часть материалов проекта размещена на местном Форуме. Материал в достаточной мере проиллюстрирован. Для просмотра иллюстраций пользуйтесь кнопкой "Открыть спойлер". Приглашаем энтузиастов принять участие в проекте.
Просмотров: 296 |
Добавил: aleksandr128 |
Дата: 03 Сентябрь 2013
|
|
В этот раз я решил максимально возможно усложнить задачу для себя в моделировании - построить модель восьмивекторного листа Мёбиуса с развязкой самопересечения. "Браслет" усложненный. Модель была выполнена по схеме восьмивекторной ленты Мёбиуса с закрутом в 3 1/8 оборота (1 125 град.).
Просмотров: 481 |
Добавил: aleksandr128 |
Дата: 26 Август 2013
|
|
Предыдущий материал позволил прояснить такую картину: классическая лента Мёбиуса может закручиваться таким образом, что будет пересекать саму себя по средней линии, создавая при этом различные по степени сложности варианты При этом все эти варианты остаются примерами односторонней поверхности со всеми присущими ей основными свойствами.
В качестве примера приведу более сложный случай самопересечения ленты Мёбиуса, где она уже дважды самопересекает саму себя (напоминаю - по средней линии). Этот вариант не встречался в Сети и смоделирован совместными усилиями с Tyomich'ем.
Остается только сделать попытку использовать такие примеры для создания различных инновационных девайсов.
 
Просмотров: 427 |
Добавил: aleksandr128 |
Дата: 23 Август 2013
|
|
Просмотров: 363 |
Добавил: aleksandr128 |
Дата: 21 Август 2013
|
|
| |
 | |  |
|
| Поиск |
|
|
| Календарь |
| « Июнь 2017 » | | Пн | Вт | Ср | Чт | Пт | Сб | Вс | | | | | 1 | 2 | 3 | 4 | | 5 | 6 | 7 | 8 | 9 | 10 | 11 | | 12 | 13 | 14 | 15 | 16 | 17 | 18 | | 19 | 20 | 21 | 22 | 23 | 24 | 25 | | 26 | 27 | 28 | 29 | 30 |
|
|
| Архив записей |
|
|
|
