|
Вокруг катушки Мёбиуса
|
|
| aleksandr128 | Дата: Пятница, 16 Мая 2014, 15:40 | Сообщение # 1 |
 Генералиссимус
Группа: Администраторы
Сообщений: 148
Статус: Offline
| По многочисленным  просьбам посетителей проекта "Геометрия ленты Мёбиуса" . Спрашивайте, высказывайте своё ПМСМ, советуйте. просьбам посетителей проекта "Геометрия ленты Мёбиуса" . Спрашивайте, высказывайте своё ПМСМ, советуйте. 
Все равно всего на всех не хватит...
|
| |
|
|
| aleksandr128 | Дата: Понедельник, 09 Июня 2014, 18:53 | Сообщение # 2 |
 Генералиссимус
Группа: Администраторы
Сообщений: 148
Статус: Offline
| Ну вот, ещё один участник проекта изъявил желание изготовить трехвекторную трехсекционную катушку Мёбиуса. Если его энтузиазм не угаснет и он доведет начатое до логического конца, то это будет третий из известных мне случаев (включая меня) изготовления трехвекторки. Пока мне известны только два готовых девайса.
Все равно всего на всех не хватит...
|
| |
|
|
| aleksandr128 | Дата: Понедельник, 09 Июня 2014, 19:33 | Сообщение # 3 |
 Генералиссимус
Группа: Администраторы
Сообщений: 148
Статус: Offline
| И ещё. Данная трехвекторка по сути является двухфазной катушкой Мёбиуса. Но на базе каркаса трехвекторки возможно изготовить упрощенный вариант трехфазной катушки Мёбиуса. При желании могу проконсультировать в частном порядке.
Сам не берусь за это дело по простой причине. Уже изготовил три девайса по этой тематике, а оснастки для эксов по полной программе нет. Делать еще один девайс чтобы просто положить его в ящик? Не вижу смысла. Могу взяться за работу на заказ. Обращаться по данному предложению через личку или "мыло".
Все равно всего на всех не хватит...
|
| |
|
|
| aleksandr128 | Дата: Среда, 02 Июля 2014, 21:03 | Сообщение # 4 |
 Генералиссимус
Группа: Администраторы
Сообщений: 148
Статус: Offline
| Пришла некоторая информация от друга, который изготовил трехвекторную катушку Мёбиуса с каркасом из оргстекла, т.е. в чистом виде, без железа.
Он пожаловался, что в режиме противохода (встречная схема включения секций) очень слабо проявляется свойство "монопольности".
Посоветовал ему для увеличения проявления "монопольности" создать некое подобие магнитопровода между секциями обмотки. Для этого надо имеющийся зазор между секциями обмотки, по всему периметру, заполнить железными штырьками. Для этого можно использовать гвоздики необходимого диаметра и длины.
Все равно всего на всех не хватит...
|
| |
|
|
| aleksandr128 | Дата: Пятница, 15 Августа 2014, 00:32 | Сообщение # 5 |
 Генералиссимус
Группа: Администраторы
Сообщений: 148
Статус: Offline
| Две трехвекторные катушки Мёбиуса. Слева - ТКМ Сергея, справа - моя ТКМ. Для сравнительного анализа.
  ТКМ ТКМ Сергея ТКМ Александра Габаритные размеры одинаковы. У обеих индексКМ=+7/3.Различия: 1. У катушки Сергея каркасные элементы из оргстекла, а несущее кольцо из латуни. У меня и то, и другое - из железа. 2. У ТКМ Сергея отсутствует средняя секция обмотки. 3. Обмотка ТКМ Сергея выполнена проводом марки МГТФ сечением 0,3мм. Обмотка моей ТКМ выполнена проводом сечением 0,1мм в тефлоновой изоляции. 4. Активное сопротивление секций обмотки у катушки Сергея примерно по 10 Ом. Активное сопротивление двух крайних секций у моей катушки примерно по 25 Ом.
Оргстекло - малопригодный материал для каркасных элементов из-за своей низкой термостойкости. По словам Сергея, при пропускании через секции обмотки пульсирующего тока силой в 0,8А температура обмотки поднимается до 67-68 градусов.
А сейчас непосредственно о эксе Сергея.
Его с самого начала заинтересовало моё сообщение, что трехвекторка, включенная в режим пульсирующего "монополя", оказывает локальное воздействие на облачность над местом нахождения работающей ТКМ.
В июле, будучи в отпуске, он одну неделю провел в деревне, вдалеке от индустриальных центров. Погода благоприятствовала проведению испытания: из семи проведенных в деревне дней, пять- со сплошной облачностью и небольшой дождливостью. В эти облачные дни он включал свою ТКМ в режим и получал неизменный результат: примерно на сороковой-сорок пятой минуте в сплошной облачности начинал образовываться просвет. Катушка в каждом случае работала чуть более часа, а затем выключалась (из-за перегрева). После этого просвет держался несколько часов и постепенно затягивался. Т.е. результат его испытаний практически совпал с моим. Вот такое было от него сообщение.
Все равно всего на всех не хватит...
|
| |
|
|
| bormihael | Дата: Суббота, 24 Января 2015, 16:51 | Сообщение # 6 |
|
Группа: Удаленные
| Цитата aleksandr128 (  ) высказывайте своё ПМСМ, советуйте. Александр, Мы с Вами встречались. С моей стороны, предложение такое - оставте крылья бабочки в несколько слоёв (3-4), Вы получите и положетельную и отрицательную , и т.д. энергий, разворачивая спираль в ту или иную сторону. С ув. Михаил33. |
| |
|
|
| aleksandr128 | Дата: Воскресенье, 25 Января 2015, 19:36 | Сообщение # 7 |
 Генералиссимус
Группа: Администраторы
Сообщений: 148
Статус: Offline
| Уважаемый bormihael, примерно такие особенности, и даже в большей мере, предусмотрены в работе трехфазной катушки Мёбиуса. Особенно при веерном режиме работы.
Я не приступал к ее изготовлению по простой причине. Изготовить такую катушку относительно просто. Основная сложность - аппаратное ( питание) обеспечение.
Все равно всего на всех не хватит...
|
| |
|
|
| aleksandr128 | Дата: Воскресенье, 27 Декабря 2015, 02:40 | Сообщение # 8 |
 Генералиссимус
Группа: Администраторы
Сообщений: 148
Статус: Offline
| Изготовление каркаса катушки Мёбиуса вручную - это конечно очень заморочно. И, как мне видится, это одно из основных препятствий получения такой катушки. Но с появлением 3-D принтеров эта задача облегчается.
Мы с Tyomich'ем сделали попытку создать файл прототипа каркаса катушки М для 3-D печати с практически идеальной геометрией. Представленный ниже вариант каркаса трехвекторной катушки Мёбиуса, после минимальной доработки, можно превратить в каркас трехфазной катушки (для получения эффекта электромагнитной воронки).
Собственно один из вариантов каркаса трехвекторной катушки Мёбиуса по индексуКМ=+8/3 (с правозаходным закрутом в 22/3 оборота):


Все равно всего на всех не хватит...
|
| |
|
|
| aleksandr128 | Дата: Суббота, 09 Июля 2016, 02:25 | Сообщение # 9 |
 Генералиссимус
Группа: Администраторы
Сообщений: 148
Статус: Offline
| Доступно только для пользователей
Все равно всего на всех не хватит...
|
| |
|
|
| Садовник | Дата: Суббота, 13 Января 2018, 16:30 | Сообщение # 10 |
|
Рядовой
Группа: Пользователи
Сообщений: 3
Статус: Offline
| Цитата aleksandr128Цитата Закрытый тор заинтересовал меня по той простой причине, что, на мой взгляд, область самопересечения является как-бы проекцией четырехмерной части пересечения в наше трехмерное пространство. Другими словами: часть закрытого тора принадлежит трехмерному пространству, а часть уходит в чтырехмерное.
Планирую попытаться сконструировать такой девайс, где с помощью катушки Мёбиуса и катушечного контура закрытого тора, создать в области самопересечения такое взаимодействие электормагнитных полей, что хрен его знает... "как-бы, где-то, местами потревожить четвертую мерность". Продолжить эту тему планирую на ветке "Девайсы...".
Такой вопрос: а где может использоваться 4D? Знаю, что многомерные таблицы используются в статистике для анализа данных. А где ещё могут использоваться высшие размерности?
С уважением, Gyfto.Добавлено (13 Январь 2018, 09:19)
---------------------------------------------
Поясню свои мотивы. В последние годы одно из активных и многообещающих направлений исследований - это многомерная геометрия. Многообещающих - чем? В чём могут быть полезны эти исследования? Не поймите превратно, это не сарказм, а определение целей. Добавлено (13 Январь 2018, 16:30)
---------------------------------------------
Я правильно понимаю, что аналогом 4D-пространства является внутреннее пространство любого процессора, где у каждой внутренней точки своя вольт-амперная характеристика? Насколько я помню книгу Шинтана Яу по теории струн, он писал, что четвёртая координата это заряд. Но 3D-фигура с потенциалом в каждой её точке - это 3D-плоскость в 4D-пространстве, а не 4D-пространство. У круга или леминискаты Бернулли уже две точки по оси абсцисс. Как точка может иметь два заряда одновременно? А вот если добавить пятую координату и договориться о том, что начало координат плоскости Ox4x5 лежит в каждой точке 3D-пространства, то получим полноценную 3D-проекцию 4D-пространства. К примеру, возьмём любой однокристальный компьютер, например, модный нынче стик (HDMI-мини-компьютер). В каждой точке 3D-пространства кристалла своя нелинейная вольт-амперная характеристика. Я вот точно не знаю (образование не то), у мозга тоже своя кривая ВАХ в каждой 3D-точке? Получаем мысленно представимое 4D-пространство. Правильно я понимаю? Тогда 4D-геометрию (и 4D-лМ) можно использовать в схемотехнике.
|
| |
|
|
| aleksandr128 | Дата: Суббота, 13 Января 2018, 18:07 | Сообщение # 11 |
 Генералиссимус
Группа: Администраторы
Сообщений: 148
Статус: Offline
| Здравствуйте Gyfto.
Вопрос, с которым Вы обратились ко мне, весьма сложен и вряд ли я смогу ответить на него однозначно.
У меня есть определенная "картинка" по этой проблеме. Но... Во-первых - я вообще то дилетант и в одиночку не потяну такую тему, а во-вторых - достаточно ленив, чтобы стучать по клаве, в надежде озвучить свою дилетантскую "картинку"...
Еще Тютчев Ф.И. в своем гениальном стихотворении "Siilentium" высказал замечательную мысль:
"...Как сердцу высказать себя? Другому как понять тебя? Поймет ли он, чем ты живешь?.. Мысль изреченная есть ложь..."
Максимум на что я могу сподвигнуться по заданному вопросу - это озвучить свой взгляд на эту проблему в приватной беседе по Скайпу. Я отправил Вам в личку свой позывной в Скайпе. Будет желание - звоните.
Все равно всего на всех не хватит...
|
| |
|
|
| Садовник | Дата: Воскресенье, 14 Января 2018, 12:49 | Сообщение # 12 |
|
Рядовой
Группа: Пользователи
Сообщений: 3
Статус: Offline
| Цитата aleksandr128 (  ) Вопрос, с которым Вы обратились ко мне, весьма сложен и вряд ли я смогу ответить на него однозначно.
Прошу прощение, накипело. За державу обидно...
Цитата Садовник (  ) Правильно я понимаю?
1) Одно ВАХ-сечение описывает один край фигуры, либо одну плоскость (мембрану). У несамопересекающейся фигуры два края, т.е. для её представления нужен двухполюсный полупроводниковый прибор. Для самопересекающейся уже четырёхполюсный и выше. Вот пример представления 3D-фигуры на 2D(xy)+2D(UI)-плоскостях:
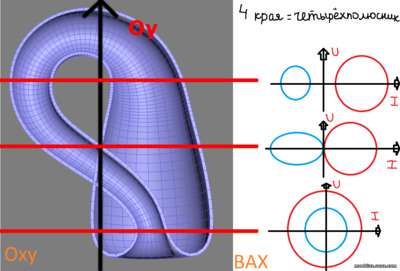
Ещё раз повторю: круг в этой трактовке имеет два края, потому что каждому значению по оси абсцисс сопоставляется два значения по оси ординат.
2) Из возможности мысленного схемотехнического представления 4D-пространства вовсе не следует возможность использования 4D-моделей в схемотехнике.Добавлено (14 Январь 2018, 12:49)
---------------------------------------------
По-идее, тандема 1*3D(xyz)+1*2D(UI), где 2D(UI)-плоскость перпендикулярна любой координатной плоскости 3D-пространства, достаточно для описания 4D-фигуры, но я переспрошу на матфоруме.
|
| |
|
|
| aleksandr128 | Дата: Воскресенье, 14 Января 2018, 18:51 | Сообщение # 13 |
 Генералиссимус
Группа: Администраторы
Сообщений: 148
Статус: Offline
| В своих работах по ленте Мёбиуса (далее - лМ) мы с Тёмичем пользовались программой SolidWorks. Для просмотра созданного материала можно использовать бесплатное приложение к программе под названием eDrawings. Если у Вас есть такое приложение, то по желанию мы можем скинуть любой файл по по теме лМ. Несколько примеров 3-D визуализации лМ выложены в в раделе Видео .
Все равно всего на всех не хватит...
|
| |
|
|
| Садовник | Дата: Суббота, 20 Января 2018, 20:43 | Сообщение # 14 |
|
Рядовой
Группа: Пользователи
Сообщений: 3
Статус: Offline
| aleksandr128, а на сферу лМ спиралью намотать не пробовали? Получается площадка радиусом в ширину лМ на одном полюсе, звезда пересечений рёбер лМ на другом и гармошка параллельных(?) лМ между ними. У такой сферы Мёбиуса (можно?), кроме того, что она односторонняя, есть ещё одно необычное свойство: её можно вращать вокруг своего цента (а не только вокруг своей оси, как обычную сферу). Получаем всенаправленную центрифугу. Вот только характер взаимоотношений между соседними лМ остаётся неясным. На "звёздном" полюсе лМ не параллельны, а радиальны друг другу, т.е. пересекаются внутри сферы (если продлить их плоскости до линии пересечения). Около "плоского" полюса они параллельны друг другу. Так параллельны или пересекаются? Какой характер у пространства внутри сферы Мёбиуса?
А на матфоруме молчание. Придётся доказывать либо опровергать своё предположение своими мозгами.Добавлено (20 Января 2018, 20:43)
---------------------------------------------
Цитата Садовник (  ) спиралью намотать не пробовали?
Цитата Садовник (  ) (если продлить их плоскости до линии пересечения). |
| |
|
|
| aleksandr128 | Дата: Суббота, 20 Января 2018, 21:00 | Сообщение # 15 |
 Генералиссимус
Группа: Администраторы
Сообщений: 148
Статус: Offline
| Уважаемый Садовник , при исследовании свойств лМ , я пришел к выводу, что две (или больше) лМ, при взаимном пересечении образуют двух- или более -стороннюю поверхность. Только при самопересечении лМ сохраняет свойство односторонности.
К следующему посту я подготовлю иллюстрации, наглядно демонстрирующие этот вывод. Как подтверждение данного вывода можно привести бутылку Кляйна. Она состоит из двух лМ с разнонаправленной закрученностью (лево- и правозаходная). В эвклидовом пространстве без взаимопересечений не обойтись. Это касается и лМ, закрученных в одну сторону.
В нашем приватном разговоре по Скайпу я подчеркивал, что нельзя создать две взаимопараллельных лМ.
Поэтому я считаю, что сфера Мёбиуса - это нонсенс.
Все равно всего на всех не хватит...
|
| |
|
|
|







