В предыдущих заметках о самопересекающихся поверхностях я подчеркивал, что для лучшего восприятия некоторых особенностей самопересекающейся ленты Мёбиуса удобно использовать креативный подход. Т.е. моделировать не просто абстрактную математическую поверхность, в которой не искушенному читателю весьма затруднительно разбираться, а создавать модель, по которой намного легче понять скрытые нюансы геометрии предлагаемого к рассмотрению объекта.

  В качестве примера позволю себе напомнить предыдущую модель 2-хвекторной ленты Мёбиуса с базовым углом закрута в 270⁰. Чтобы подчеркнуть, что это обычная, "классическая", лента Мёбиуса, только закрученная не на полоборота, а на три четверти, линия самопересечения убрана с помощью отверстий. Количество отверстий не лимитировано - от одного (см. предыдущую заметку по теме) и далее...

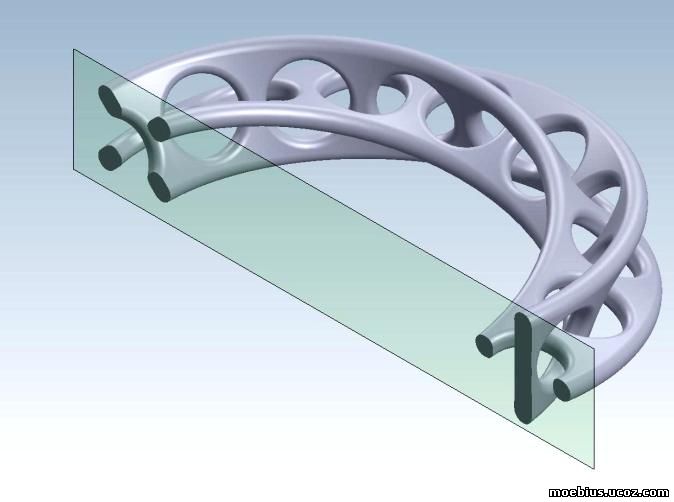
  Используя такой подход, были промоделированы варианты 2-хвекторной ленты Мёбиуса с различными углами закрута. Изображения этих моделей  можно найти в предыдущих заметках Ленты Новостей. Для удобства они названы браслетами Мёбиуса.

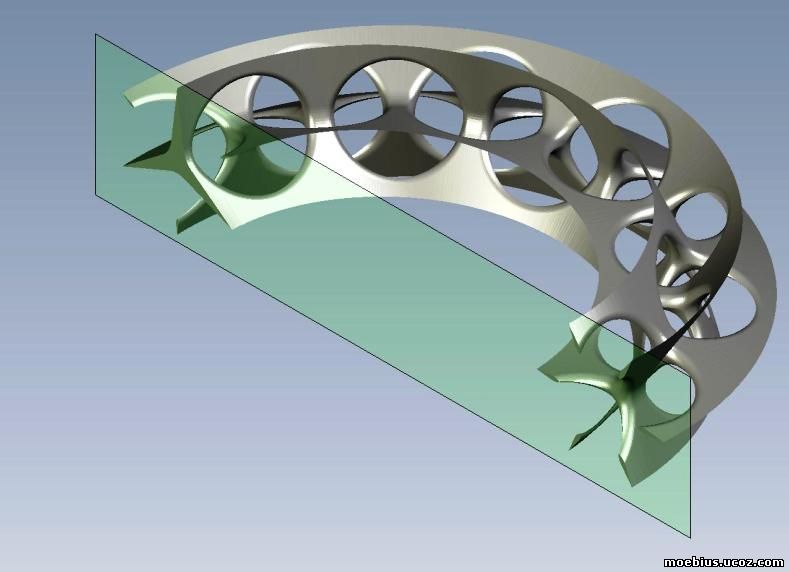
  Для того, чтобы убедиться,что 3-хвекторная лента Мёбиуса - это не "бред сивого мерина", с неоценимой помощью Tyomich'a, была создана графическая 3-D модель самопересекающейся трехвекторки, решенная в этом же ключе. Базовый угол закрута - 60⁰ (индекс_кМ=+1/6):

  Вопросы и замечания можно оставлять здесь же, в разделе "комментарии" или в "Гостевой книге".